
点乘:两个向量点乘得到一个标量 ,数值等于两个向量长度相乘后再乘以二者夹角的余弦值 。如果两个向量a,b均 为单位 向量 ,那么a.b等于向量b在向量a方向上的投影的长度
点乘后得到的是一个值
若结果 == o,则 两向量 互垂直 。
若结果 < 0 ,则 两向量夹角大于90°。 若结果 >0 ,则两向量夹角小于 90°。叉乘:两 个向量的叉乘得到一个新的向量 ,新向量垂直于原来的两个向量再乘夹角的正弦值
叉乘后得到的还是一个向量
在里面。两个向量的点乘所得到的是两个向量的余弦值,也就是-1 到1之间,0表示垂直,-1表示相反,1表示相同方向。 两
个向量的叉乘所得到的是两个向量所组成的面的垂直向量,分两个方向。 简单的说,点乘判断角度,叉乘判断方向。 形象的说当一个
敌人在你身后的时候,叉乘可以判断你是往左转还是往右转更好的转向敌人,点乘得到你当前的面朝向的方向和你到敌人的方向的所
成的角度大小。
为了理解以上问题我们先了解一下Sin和Cos两个数学函数;
1、Sin和Cos的基础知识:
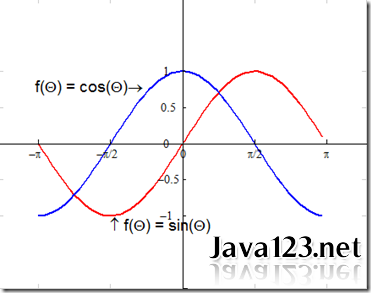
Sin函数:
取值范围是-1到1.
注意:
sin(0) = 0;
sin(90) = 1;
sin(180) = 0;
sin(270) = -1;
sin(360) = 0;
由此我们得到 0--180 为正数,180--360取负数;
度数如为负数,则与之相反如下:
sin(0) = 0;
sin(-90) = -1;
sin(-180) = 0;
sin(-270) = 1;
sin(-360) = 0;
Cos函数:
取值范围是-1到1.
注意:
cos(0) = 1;
cos(90) = 0;
cos(180) = -1;
cos(270) = 0;
cos(360) = 1;
由此我们得到 0--90,270 -- 360 为正数,90 --270取负数;
度数如为负数,与之相同如下:
cos(0) = 1;
cos(-90) = 0;
cos(-180) = -1;
cos(-270) = 0;
cos(-360) = 1;
2、在了解sin和cos的基础知识后,我们来看一下叉乘和点乘的公式;
以上我们了解,点乘的结果是一个浮点数
点乘公式:
|a|*|b| * cos<a,b>
向量a、b的大小和a、b之间的cos夹角相乘。
题一:player是一个玩家,判断Enemy在player的前方或后方。
player的前方我们设为a向量,Enemy到player的向量我们设为b向量 ,所以Enemy所在前后取决于Cos夹角,如果Cos夹角得出是正数,则在前方。如为负数,则在后方。代码如下:
float dot(Vector3 a,Vector3 b) { return Vector3.Dot(a,b); }void main(){ float tmp = dot(a,b); if(tmp > 0) { Debug.Log("b在a的前方"); }else if(tmp < 0) { Debug.Log("b在a的后方"); } else { Debug.Log("b在a的正左侧或正右侧"); }}
题二:player是一个玩家,判断Enemy在player的哪个方位。
public class DotAndCross : MonoBehaviour { public Transform obj; // Use this for initialization void Start () { } float timer = 0f; float devTimer = 2f; // Update is called once per frame void Update () { if ((timer + devTimer) > Time.time) return; timer = Time.time; Vector3 tmpDir = obj.position - transform.position; Debug.Log("cross == " + cross(transform.forward, tmpDir.normalized)); } /// /// 判断方位 /// /// /// ///